Trigonometric Leveling: Comprehensive Guide For Accurate Elevation Determination

A trigonometric leveling guide provides comprehensive instructions on the principles, techniques, and applications of trigonometric leveling in surveying and construction. It covers direct and indirect leveling, trigonometric principles involving vertical angles and distances, elevation determination, vertical angle measurement, distance measurement methods, stadia rod usage, practical applications, and precision and accuracy considerations. The guide serves as a valuable resource for surveyors, engineers, and professionals seeking to master the art of trigonometric leveling for accurate elevation determination and project implementation.

Unlocking the Secrets of Trigonometric Leveling: A Guide to Elevation Determination

In the world of surveying and construction, precision and accuracy reign supreme. Enter trigonometric leveling, a technique that allows us to determine elevation, a crucial measurement in shaping our built environment.

Trigonometric leveling, as its name suggests, uses principles of trigonometry to measure vertical angles and distances, enabling us to establish the heights of points relative to a known reference datum. These measurements play a vital role in surveying projects, such as designing roads, railways, and buildings, as well as in construction, ensuring proper drainage and structural stability.

Unlike direct leveling, which involves reading elevation differences through a line of sight, trigonometric leveling offers a more versatile and efficient approach. Using instruments such as the theodolite and electronic distance meter, surveyors can determine elevation indirectly, making it ideal for measuring over long distances and obstacles.

Direct versus Indirect Leveling

In the realm of surveying and construction, determining elevations and establishing level surfaces is a crucial task. Trigonometric leveling provides a highly accurate method for this purpose, utilizing trigonometric principles to calculate elevation differences. Two primary approaches to trigonometric leveling are direct and indirect.

Direct leveling involves measuring vertical angles and distances from a known reference point to determine the elevation of a target point. The most common equipment used in direct leveling is a level and a stadia rod. The level is used to precisely determine the horizontal line of sight, while the stadia rod is marked with graduations that allow distances to be measured directly along this line of sight.

In contrast, indirect leveling involves measuring vertical angles from two known reference points to a target point without directly measuring distances. This method utilizes the principle of trigonometry to calculate horizontal distances and elevations. The equipment used in indirect leveling typically includes a total station or a theodolite, which can measure both vertical angles and horizontal directions.

The choice between direct and indirect leveling depends on the accuracy and practicability requirements of the project. Direct leveling is generally more straightforward and less expensive, but it can be less accurate over longer distances. Indirect leveling, on the other hand, provides higher accuracy but requires more specialized equipment and is more time-consuming.

Principles of Trigonometric Leveling

Trigonometric leveling is a sophisticated technique used in surveying to determine elevations with high precision. It harnesses the principles of trigonometry to calculate height differences between points on the Earth’s surface.

At the heart of trigonometric leveling lies the vertical angle. This angle measures the tilt of the line-of-sight between the surveying instrument and the target (typically a stadia rod). The distance between the instrument and the target is also crucial.

To determine elevation differences, surveyors employ basic trigonometric functions. By measuring the vertical angle and distance, they can calculate the height of the target relative to the instrument. This process is repeated at multiple points to create a vertical profile of the terrain.

By understanding these trigonometric principles, surveyors can accurately determine_elevations_ of points, whether for construction projects or surveying large areas. Trigonometric leveling remains a cornerstone of modern surveying practices, enabling precise mapping and detailed elevation data.

Vertical Angles in Trigonometric Leveling

• Define vertical angles and explain how they are measured
• Discuss their role in determining elevations

Vertical Angles in Trigonometric Leveling

In trigonometric leveling, vertical angles play a crucial role in determining elevations. They measure the angle between the horizontal line of sight and the inclined line of sight to the staffor (a graduated rod).

To measure vertical angles, a theodolite or total station is used. These instruments provide precise angle measurements in both the horizontal and vertical planes. The vertical angle is read from the theodolite’s vertical circle or the total station’s vertical compensator.

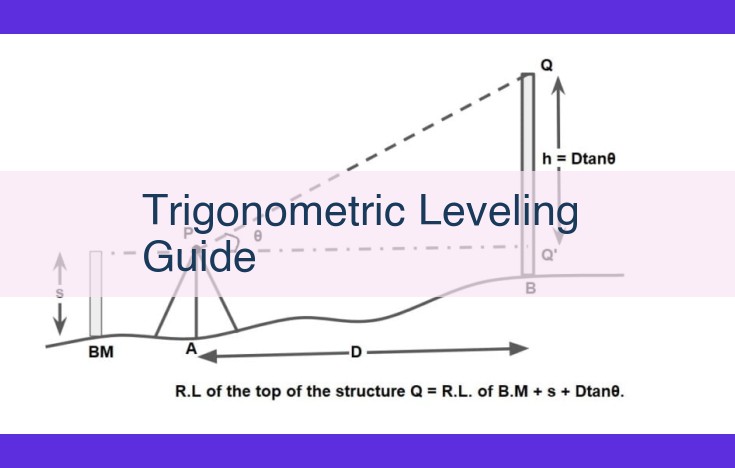
Vertical angles are essential for calculating elevations because they allow us to determine the height difference between the instrument and the staff. Using trigonometry, we can calculate the vertical distance (h) using the formula:

h = distance * tan(vertical angle)

For example, if we measure a vertical angle of 25 degrees and the distance to the staff is 100 feet, the height difference would be:

h = 100 ft * tan(25 degrees) = 46.98 ft

By knowing the height difference and the instrument height (the height of the instrument above the ground), we can calculate the elevation of the staff:

Elevation of staff = instrument height + height difference

Vertical angles are crucial in trigonometric leveling because they allow us to determine elevations with precision. The accuracy of the results depends on the precision with which the vertical angles are measured. Therefore, it is essential to use reliable equipment and follow best practices for accurate angle measurements in trigonometric leveling.

Distance Measurement in Trigonometric Leveling

In the realm of trigonometric leveling, distance measurement plays a pivotal role in determining elevations with precision. Accurate distance measurements are essential for reliable elevation calculations.

Several methods are employed for distance measurement in trigonometric leveling, each with its own advantages and limitations.

• Taping or Chaining: This traditional method involves physically measuring the distance between points using a tape measure or chain. It provides high accuracy in short distances but can be time-consuming and impractical for longer distances.

• Electronic Distance Measurement (EDM): EDM instruments use electromagnetic waves to measure distances instantaneously and accurately. They offer greater range and convenience than taping or chaining, making them ideal for large-scale projects. However, environmental conditions can affect EDM accuracy.

• Stadia Lines: Used in conjunction with a theodolite or level, stadia lines are marked on a graduated rod held at the reference point. By measuring the vertical angle between the stadia lines, the horizontal distance can be calculated. This method is less accurate than other methods but can be useful in estimating distances quickly.

Factors affecting accuracy in distance measurement include:

• Instrument quality: Using high-quality instruments is crucial for precise measurements.
• Environmental conditions: Temperature, humidity, and atmospheric pressure can influence electromagnetic wave propagation in EDM.
• Operator skills: Proper calibration and handling of instruments are essential for reliable results.

Ensuring precision and accuracy in distance measurement is paramount in trigonometric leveling. By selecting the appropriate method and accounting for potential error sources, surveyors can obtain accurate elevation data that is essential for various surveying and construction projects.

Elevation in Trigonometric Leveling

Understanding Elevation: The Bedrock of Surveying

Elevation, the vertical distance above a reference point, is the cornerstone of both surveying and construction. It determines the precise height of structures, ensures proper drainage, and aids in land development planning.

Reference Datums: The Foundation of Elevation

To establish elevations accurately, we rely on reference datums: established surfaces used as benchmarks. The Mean Sea Level (MSL), a universally accepted reference, serves as the zero point for elevation measurements worldwide. Other datums, such as the North American Vertical Datum of 1988 (NAVD88), provide local reference points for specific regions.

Establishing Elevations: From Reference to Reality

Establishing elevations involves measuring the vertical distance between known points and the reference datum. Trigonometric leveling, with its precise angle and distance measurements, plays a crucial role in this process. Through meticulous observations and calculations, surveyors determine the elevation of survey points, providing a precise understanding of the terrain’s vertical configuration.

The Stadia Rod: A Guiding Tool in Trigonometric Leveling

In trigonometric leveling, a stadia rod is an indispensable tool that plays a pivotal role in determining distances. This slender, graduated rod, adorned with contrasting markings, serves as a visual guide for precise distance measurements.

The stadia rod is typically constructed of lightweight but durable materials, such as fiberglass or aluminum, making it easy to handle and transport. Its surface is marked with target points, which are horizontal lines that divide the rod into equal intervals. These target points, when viewed through a leveling instrument, create an optical illusion that allows for accurate distance estimation.

In trigonometric leveling, the stadia rod is held vertically at a known distance from the leveling instrument. By observing the intersection of the stadia lines with the target points, the surveyor can calculate the distance between the instrument and the rod using trigonometric principles. This technique, known as stadia distance measurement, provides a convenient and efficient way to obtain distances without the need for direct measurement.

The accuracy of stadia distance measurement depends on several factors, including the precision of the leveling instrument, the distance between the instrument and the rod, and the observer’s skill. To ensure accuracy, surveyors must carefully calibrate their instruments and adhere to established best practices for data collection.

Trigonometric Leveling in Practice: Real-World Applications

In the world of surveying and construction, trigonometric leveling plays a pivotal role in determining elevations and establishing vertical control. This technique provides precise measurements of heights and distances, enabling professionals to design and build structures with unmatched accuracy.

Surveying Applications

Trigonometric leveling is essential for establishing elevation benchmarks and creating topographic maps. Surveyors use this method to:

• Determine the height of natural features, such as mountains and valleys
• Establish elevations for property boundaries and construction sites
• Create topographic maps that visualize the terrain’s contours and slopes

Construction Applications

In construction, trigonometric leveling is indispensable for:

• Setting the foundation and framing of buildings to ensure level and stable structures
• Installing utilities, such as pipelines and power lines, with precise elevations and gradients
• Monitoring the progress of construction projects to ensure adherence to design plans

Project Implementation Examples

• Bridge Construction: Trigonometric leveling was used during the construction of the iconic Golden Gate Bridge, ensuring that the towers were erected at the exact same elevation across the San Francisco Bay.
• Dam Building: The Hoover Dam’s massive concrete structure required precise elevation measurements using trigonometric leveling to maintain its stability and prevent water seepage.
• Highway Design: For the winding roads of the Swiss Alps, trigonometric leveling played a critical role in determining the gradients and elevations, ensuring safe and efficient travel.

Trigonometric leveling, with its precise measurements and wide-ranging applications, is a cornerstone of accurate surveying and construction. By understanding its principles and practical uses, professionals can unlock the power of this versatile technique to create structures that stand the test of time and shape our built environment.

Precision and Accuracy in Trigonometric Leveling

In the realm of surveying and construction, trigonometric leveling plays a crucial role in determining elevations and distances. While precision and accuracy are paramount for reliable results, it can be challenging to achieve both consistently. In this section, we’ll delve into the importance of precision and accuracy in trigonometric leveling and provide valuable guidance on best practices for successful implementation.

Defining Precision and Accuracy

Precision refers to the consistency of measurements, while accuracy reflects their closeness to the true value. In trigonometric leveling, precision is often expressed as the standard deviation of the measurements, indicating the spread of data around the mean. Accuracy, on the other hand, is determined by comparing the measured elevations with known control points or reference benchmarks.

Importance of Precision and Accuracy

Precise and accurate measurements are essential for numerous reasons. In surveying, precise elevation data is vital for accurate mapping and topographic modeling. In construction, accurate elevation control ensures proper drainage, structural stability, and adherence to design specifications. Errors in either precision or accuracy can lead to costly rework, delays, and potential safety hazards.

Best Practices for Successful Implementation

Achieving both precision and accuracy in trigonometric leveling requires adherence to certain best practices:

• Use high-quality equipment: Invest in well-calibrated levels, theodolites, and stadia rods to minimize instrumental errors.
• Follow established procedures: Adhere to standardized leveling techniques and maintain proper field documentation to ensure consistency and reduce human errors.
• Minimize external influences: Avoid environmental factors that can affect measurements, such as atmospheric conditions, vibrations, and unstable ground.
• Establish reliable control points: Use known control elevations as reference benchmarks to increase accuracy.
• Perform multiple measurements: Take multiple readings and calculate an average to improve precision and minimize the impact of any single outlier.
• Proper instrument setup: Ensure that the level is properly leveled and the theodolite is accurately calibrated for vertical angle measurements.

Precision and accuracy are the cornerstones of successful trigonometric leveling. By adhering to the best practices discussed above, surveyors and construction professionals can confidently obtain reliable elevation and distance data for accurate mapping, construction, and engineering projects. Remember, the integrity of your measurements depends on the precision and accuracy with which they are taken.